Solución del problema de geometría analítica por semejanza de triángulos

Problema resuelto de geometría analítica: el alumno desmotivado.

El enunciado queda gráficamente expresado en la siguiente imagen:

Se nos pide determinar en qué punto de la pared impacta la pelota, punto al que nos referimos arbitrariamente como P (0, y, z).

Como queda expuesto en la figura anterior, observamos que la trayectoria de la pelota inscribe dos triángulos semejantes. De forma que podemos aplicar la semejanza de triángulos. Calculamos los vectores que unen los puntos relevantes:

Lo que hemos hecho ha sido expresar la ecuación de la recta r en forma paramétrica utilizando un punto perteneciente a dicha recta C, y el vector director de r, v = (0, a, –1).

Así hemos ubicado las coordenadas del punto P (0, aλ, 2 – λ).

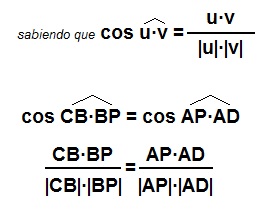
A continuación aplicamos el teorema de semejanza de triángulos con los módulos de los vectores determinados anteriormente:

Reordenamos los términos de esta igualdad de dos incógnitas (a, λ) igualándola a cero, y ha de quedarnos la siguiente ecuación:

(5a² + 5) λ² + (8a² + 8) λ – (4a² + 4) = 0

Ahora debemos despejar la incógnita λ y resolver la ecuación de 2º grado resultante en función de la otra incógnita a. Es un paso sencillo pero trabajoso. La ecuación nos da, obviamente, dos soluciones.

λ₁ = -2

λ₂ = 0,4 = 2/5

Escogemos la segunda solución λ₂ = 2/5, puesto que no tendría sentido que la pelota rebotase por debajo del suelo.

Con esta raíz volvemos a las coordenadas del punto P (0, aλ, 2 – λ), y sustituimos el valor obtenido.

Por lo tanto, las coordenadas finales del punto P y, por tanto, la respuesta al ejercicio:

P (0, 2/5a, 3/5)

Expresando las coordenadas en función de la distancia a (dirección Y), que no la podemos conocer, a menos que la pelota hubiera descascarillado la pared al impactar y, posteriormente, pudiésemos medir con un metro la distancia desde la pared frontal hasta la marca. Lo que hacemos en este caso es escoger un valor arbitrario para a, el más sencillo.

Si a = 1, entonces P (0, 2/5, 3/5)

Lo que debemos concluir con esto, no es que resulta imposible calcular el punto exacto donde la pelota impacta contra la pared izquierda conociendo únicamente el punto de inicio y el punto de llegada, no, sino que dicho punto solo depende de esas otras coordenadas. En otras palabras, la pelota se comparta como cualquier partícula, y queda demostrado que el ángulo de incidencia equivale al ángulo de rebote.

Por esta conclusión podemos comprobar que habríamos obtenido el mismo resultado aplicando, en lugar del teorema de semejanza de triángulos, la fórmula relativa a la igualdad de ángulos. Es decir,