Problema resuelto: campo eléctrico debido a un plano indefinido cargado uniformemente con dos distribuciones de carga del mismo valor pero signos opuestos.

Cuando estudiaba electromagnetismo en la facultad, o cualquier otra asignatura de Ciencias Físicas, solía preguntarme la utilidad de los cientos de problemas propuestos. Por un lado, tenemos la finalidad inmediata. Dado que no existe un truco mágico para aprobar los exámenes, el único secreto consiste en resolver problemas como un loco, cada día, al menos cinco de cada materia. Primero para coger soltura y segundo porque existen decenas de supuestos diferentes para cada apartado. Por otro lado, la finalidad última estriba en conocer la aplicación real de esas fórmulas.
A modo de ejemplo voy a proponer un problema. Utilizamos este problema para determinar el campo eléctrico debido a un plano indefinido, obviamente cargado. Una vez conocemos esto, podemos deducir las fórmulas necesarias que nos llevarán a determinar la cantidad de energía eléctrica almacenada por un condensador.
¿Qué es un condensador?
Tenemos un caso físico real, el condensador, que consiste en un dispositivo compuesto por dos conductores planos cargados y enfrentados. Ambas cargas poseen el mismo valor pero signos opuesto, -Q y +Q. Este dispositivo sirve para almacenar una cantidad determinada de energía eléctrica debida al campo eléctrico generado entre las placas.
También denominados capacitadores, normalmente en su interior disponen de dos placas conductoras separadas por un material dieléctrico. Funcionan de la siguiente manera: conectamos el condensador a una fuente de voltaje, por ejemplo una batería, entonces empieza a circular corriente eléctrica a través del circuito, y las placas se cargan positiva y negativamente. A continuación, retiramos la fuente de alimentación. Ahora, si conectamos una resistencia al condensador, este comenzará a descargarse.
La capacidad C de un condensador se define como el cociente entre la carga Q y la diferencia de potencia V-Vo existente entre ellos. La unidad de capacidad es el Faraday F.
De modo que lo interesante en este caso es averiguar cuánta energía podemos almacenar en función del condensador empleado. Pero antes de poder averiguarlo debemos tener algunas nociones básicas. En primer lugar, calcularíamos el campo creado por una placa plana indefinida, cargada con una densidad superficial de carga, y aplicando el teorema de Gauss.

El siguiente problema complica un poco las cosas, dado que el plano indefinido posee dos distribuciones de carga del mismo valor pero signos opuestos.
Sobre un plano indefinido tenemos dos distribuciones de carga. Una densidad superficial uniforme –σ sobre un círculo de radio R, y otra +σ sobre el resto del plano. Aplicando el principio de superposición, calcula E sobre el eje Z.
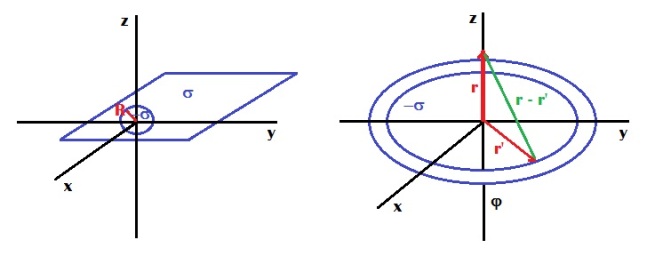
Las respectivas densidades superficiales, σ y -σ, equivalen a σ sobre todo el plano en su totalidad sustrayéndole –2σ que corresponde al círculo de radio R.
1) E debido al círculo de radio R y densidad –2σ.
Presenta simetría cilíndrica con respecto al eje Z, de modo que solo tiene componente en esa dirección (las componentes perpendiculares a Z se anulan). La carga elemental corresponde a –2σds’.
Vectores de posición:

Las componentes en la dirección paralela a Z son proporcionales a:

|z| significa que tiene el mismo módulo para z > 0 y para z < 0, pero signos contrarios:

2) E debido al plano con distribución σ.
Con un planteamiento análogo al anterior tenemos que:

Donde el vector E resulta de superponer los Ez hallados en 1) y en 2).
De esta misma forma se pueden resolver todos los problemas donde se pida el campo eléctrico debido a un plano indefinido.
